Los Griegos

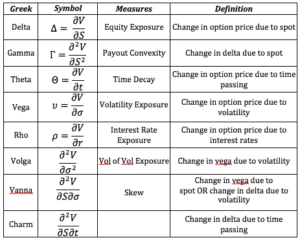
Los llamados Griegos son indicadores de la sensibilidad del precio de una opción a los factores que lo determinan, como la volatilidad o el valor del activo subyacente.

Los Griegos se utilizan en el análisis de sensibilidad de opciones y permiten a los traders medir y evaluar el impacto de cada movimiento de precio del activo subyacente en el precio de la opción. Muchos fondos de inversión basan sus estrategias en estos valores.

En términos más simples, nos ayudan a entender cómo reacciona el precio de la opción cuando el activo subyacente exhibe diferentes «comportamientos», al cambiar una o más variables mientras se mantienen otras constantes.

Sirven como indicadores para la previsión y pueden ser muy útiles, pero es esencial entender que son estimaciones teóricas y, por lo tanto, falibles.

Entiende que detrás de cada estrategia direccional hay un juego de probabilidad; el objetivo no es tener razón cada vez, sino ganar dinero. El objetivo siempre es minimizar el riesgo y maximizar el beneficio potencial.

Delta (Δ)

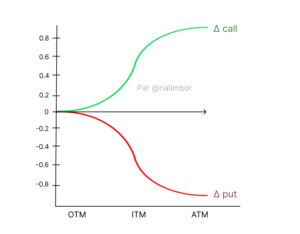
Esta es probablemente la medida que verás con más frecuencia porque es muy útil y ofrece muchas aplicaciones. Δ mide el cambio en el precio de una opción cuando el valor del activo subyacente aumenta o disminuye. En otras palabras, el valor de la opción cambiará si el mercado sube o baja 1 punto. Aquí, queremos saber cuánto cambia esta variación el precio de la opción en cuestión. Δ determina el valor de las opciones de compra (positivo) y de venta (negativo) con el mismo precio de ejercicio. El delta para una opción de venta está entre 0 y -1, y para una opción de compra, entre 0 y 1. También puede representarse como: Δ = ∂S/∂V En una estrategia de inversión bajo cobertura, Δ indica cuántas criptos necesitas comprar (o vender) para protegerte de los movimientos de precio del activo subyacente. Por ejemplo, si una opción de cripto tiene un delta de 0,45 y el precio del token subyacente aumenta en $1, el valor de la opción en ese token teóricamente aumentará en $0,45.

El delta tiene, por lo tanto, tres usos:

• Δ es una medida de riesgo que estima la variación del precio de la opción para un cambio de $1 en su activo subyacente.
• Δ le dice a los traders la razón de cobertura para hacer que una posición sea delta neutral.
• Δ también puede servir como un indicador en términos de la probabilidad de que una opción expire ITM. Sin embargo, estadísticamente, cuanto más lejos esté una opción de su fecha de vencimiento y más volátil sea, menos fiable es Δ para medir la probabilidad de que la opción expire ITM.

Theta (θ)

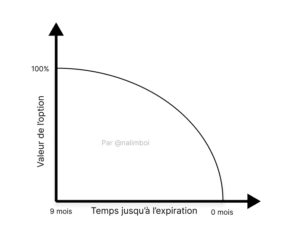
Esta variable expresa cuánto disminuirá el precio o prima de un contrato de opción con el tiempo. De hecho, el valor de una opción tiende a disminuir a medida que se acerca a su vencimiento.

Este parámetro es siempre negativo porque indica la pérdida del valor temporal de una opción, no su valor intrínseco. Es relativamente fácil observar que cuanto más lejana es la fecha de vencimiento, mayor es el valor de la opción.

Esencialmente, es una cuestión de probabilidades: la posibilidad de que la opción expire más allá del precio de ejercicio aumenta a medida que crece la incertidumbre para el vendedor de la opción en el otro lado de la operación.

Por el contrario, cuanto más cerca está la fecha de vencimiento, mayor es la probabilidad de que la opción expire OTM. Por lo tanto, puedes observar la relevancia de θ en el precio de una opción. La variable es útil para entender que el tiempo trabaja constantemente en contra del comprador de la opción y para evaluar este efecto sobre el valor de la opción.

Para tiempos cada vez más largos, cualquier opción tiene una probabilidad igualmente creciente de alcanzar su precio de ejercicio, independientemente de su valor.

Gamma (Γ)

Esencialmente cuantifica cuánto cambia el valor del activo subyacente o acción cuando cambia Delta. Por un lado, Δ da cuenta del cambio en la prima de la opción, mientras que Γ indica la tasa de cambio de Δ.

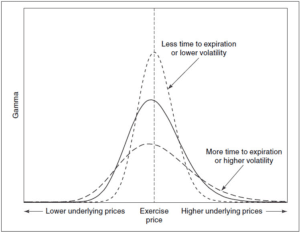
Matemáticamente, Gamma es intuitivamente la primera derivada de Delta. La letra griega es gráficamente similar a una forma log-normal de la función Delta. Así, es interesante notar que cuanto más lejano es el vencimiento, más tiende a aplanarse la curva Gamma.

Por el contrario, a medida que se acerca el vencimiento, Gamma tiende a ganar o perder valor rápidamente con cambios de precio cada vez menores, haciendo que su estructura sea más empinada y a veces incluso formando un ‘pico’ cuando el vencimiento está muy cerca. La volatilidad también juega un papel similar, manteniendo la relación: cuanto mayor es la volatilidad, más plana es la curva, y viceversa.

Rho (ρ)

Calcula el cambio en el precio de la opción causado por un aumento o disminución en las tasas de interés libres de riesgo, expresado como un porcentaje. Las opciones de venta a menudo tienen un rho negativo, mientras que las opciones de compra frecuentemente tienen un rho positivo.

Es la medida que cuantifica el cambio en el precio de la opción cuando r, la tasa de interés, también varía.

Probablemente es una de las medidas que menos varía con el tiempo; sin embargo, juega un papel importante durante las crisis o períodos de ajuste, ya que se vuelve cada vez más difícil mantener una r baja. Esto necesariamente impacta la forma en que se calcula la IV, ya que es la salida generada por la ecuación. Así, cambiar incluso una variable inevitablemente altera el resultado.

Vega (v)

Mide cómo un aumento o disminución en la Volatilidad Implícita (IV) del activo subyacente o acción modificaría el precio de la opción (prima).

En otras palabras, una mayor volatilidad esperada aumenta el valor tanto de las puts como de las calls, mientras que una menor volatilidad esperada disminuye su valor (ver la sección sobre volatilidad).

Vega tiende a prever este cambio, siendo una derivada del cambio esperado en IV.

Vega toma una forma de distribución normal y tiende a aplanarse a medida que se acerca el vencimiento.