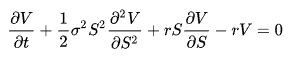Trading de Opciones

Venta de Opciones

Un error común entre los traders principiantes cuando comienzan a especular con la compra o venta de opciones es pensar que vender opciones es «dinero fácil». La razón por la que muchos caen en esta trampa es simple: según muchas fuentes, «el 90% de las opciones expiran sin valor». Veamos rápidamente por qué esta estadística es engañosa antes de introducirles en las complejidades de la venta de opciones.

De hecho, los datos del Chicago Board Options Exchange (CBOE) indican que solo el 10% de todas las opciones se ejercen realmente (la mayoría de los traders de opciones compran opciones para especular sobre su valor, no para ejercerlas sobre el valor subyacente, de ahí el bajo número), más del 60% se cierran antes del vencimiento (de nuevo, la mayoría de los traders de opciones compran opciones para especular con ellas, no para mantenerlas hasta el vencimiento), y solo alrededor del 30% expiran sin valor. Por lo tanto, vender opciones es mucho más complejo de lo que parece.

Antes que nada, un repaso sobre la naturaleza de la venta de opciones es ciertamente útil para los principiantes:

Entonces, ¿qué es vender opciones?

Recuerda la definición de una opción: es un producto que da al comprador el derecho de comprar o vender el activo subyacente si expira ITM, a cambio de una prima pagada para esperar este derecho.

En otras palabras, pagas una prima para comprar un derecho, y a la inversa, te pagan una prima cuando vendes este derecho. Esencialmente, estás expuesto a la obligación de cumplir tu parte del contrato si la opción expira ITM.

Vender una opción simplemente significa apostar a que expirará OTM, y por lo tanto sin valor. Es por eso que este producto puede ser más interesante en algunos casos que en otros.

Típicamente, entenderás que la dinámica de oferta y demanda en el mercado de opciones es similar a la de los mercados «tradicionales»: una parte hace una apuesta y paga a otra parte para que tome la apuesta opuesta. Si uno gana, el otro pierde, y así sucesivamente.

Con las opciones, factores adicionales son el tiempo y la volatilidad, que cubriremos más adelante.

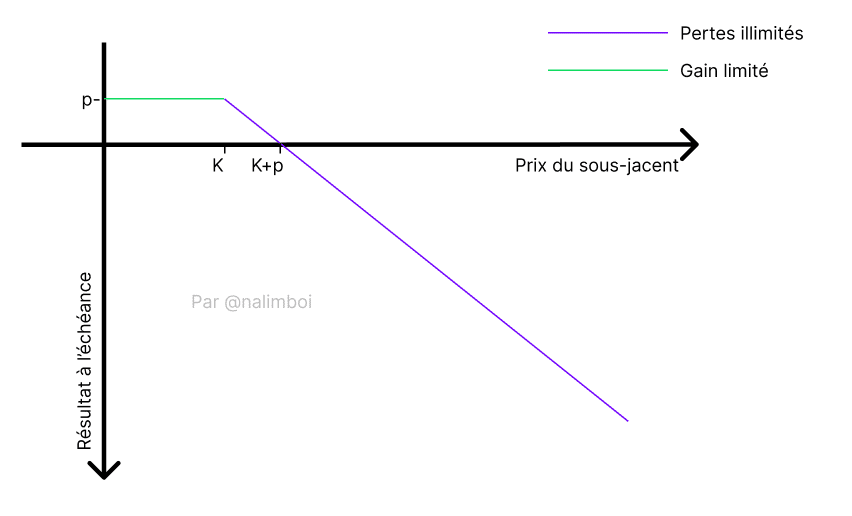
Aquí hay una representación gráfica de esta apuesta al vender una opción de compra: mientras el vendedor de la opción no vea superado el precio de ejercicio (aquí K), retiene sus ganancias de vender primas al comprador de la opción. K es el precio de ejercicio y p es la prima.

Es fácil ver que en el caso de vender opciones, las ganancias son cómodas cuando la opción expira OTM pero permanecen limitadas. A menudo, verás la expresión «recolectar primas» para indicar una venta de opción exitosa para el vendedor.

Sin embargo, las pérdidas pueden ser potencialmente ilimitadas. El peligro es principalmente creer que vender opciones representa «dinero fácil».

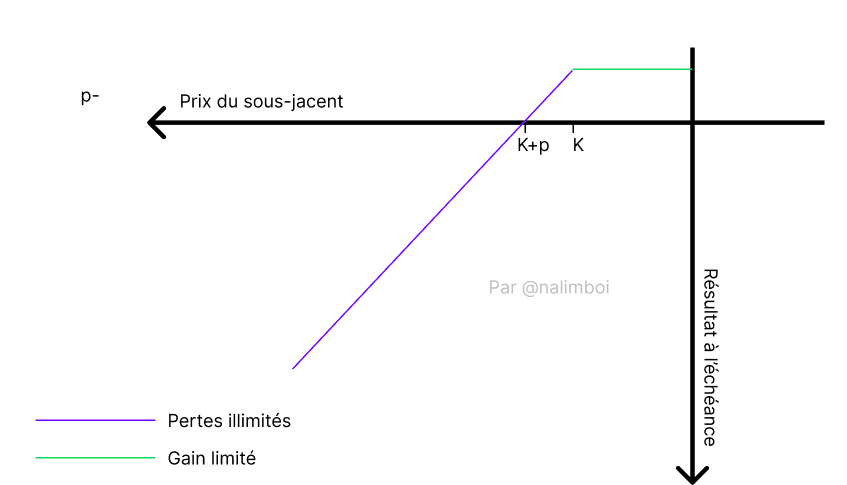
Ahora, para ver la diferencia entre las dos posibilidades de vender opciones, aquí está la de vender una opción de venta:

Entiende que vender opciones te expone en gran medida a la volatilidad, y cuanto más lejana sea la fecha de vencimiento, más probable es que tengas que cumplir tu parte del contrato.

Pero, ¿qué pasa si tu predicción resulta ser incorrecta y la opción expira ITM?

Volatilidad

De hecho, cuando especulas sobre los precios de las opciones, estás especulando principalmente sobre la volatilidad anticipada o esperada (IV = Volatilidad Implícita).

En otras palabras, cuanto mayor sea la volatilidad esperada, más caras se vuelven las opciones fuera del dinero (OTM), y lo mismo ocurre a la inversa: cuanto menor sea la volatilidad anticipada por el mercado, más caras son las opciones en el dinero (ATM).

Pero primero, volvamos a lo básico: ¿qué es la volatilidad?

Según Wikipedia, «La volatilidad es la medida de las variaciones en el precio de un activo financiero. Sirve como parámetro para cuantificar el riesgo de rendimiento y precio de un activo financiero. Cuando la volatilidad es alta, la posibilidad de ganancia es mayor, pero el riesgo de pérdida también es más alto.»

La volatilidad es un concepto que parece simple a primera vista, pero ten cuidado de no confundirla con el volumen, que son dos cosas diferentes.

La volatilidad esperada (IV) es el resultado de cálculos y la percepción general del mercado sobre los movimientos futuros en los mercados. Así, sirve como medio para protegerse contra posibles pérdidas al cubrir o para exponerse al especular y maximizar las ganancias.

Pero, ¿cómo se calcula?

A pesar de su apariencia compleja, esta ecuación es probablemente uno de los mayores avances en las finanzas de mercado modernas y permitió a los matemáticos que la formularon introducir la fijación de precios de opciones en las estrategias de los grandes actores.
Black-Scholes sirve como base para muchas formas de entender la volatilidad en los mercados. Es a partir de esta ecuación que se puede calcular la IV. Afortunadamente para ti, probablemente no necesitarás usar esta ecuación directamente, ya que muchos sitios web o aplicaciones ya se encargan de ello.
Se requieren varias condiciones para que la fórmula sea lo más cercana posible a la realidad:
Condiciones:

1. 1. 1. Los rendimientos promedio del activo estudiado deben distribuirse de manera ‘normal’ o ‘log-normal’ (ver la sección sobre la distribución normal).
      2. El mercado estudiado es eficiente, y por lo tanto, por definición, los movimientos son aleatorios (ver la sección sobre la eficiencia del mercado).
      3. Hay costos de entrada o salida mínimos o nulos; ningún actor debería ser disuadido de tomar una posición debido a las tarifas.
      4. La opción es europea, lo que significa que solo puede ejercerse al vencimiento.

Sin embargo, como podrás adivinar, estas condiciones no siempre se cumplen simultáneamente. Esto puede resultar en un cálculo de IV a veces sesgado, lo cual discutiremos más adelante.
Ahora veamos las variables involucradas en la resolución de la ecuación:

Variables:

1. 1. • r = tasa de interés libre de riesgo
        r es la tasa de interés a la que uno puede invertir y generar ingresos libres de riesgo en la economía. En la mayoría de los casos, el cálculo se realiza utilizando bonos del Tesoro, ya que representan una de las pocas inversiones ‘libres de riesgo’. Esta variable se utiliza para determinar si una estrategia es viable durante un año: si la estrategia implica riesgo y el rendimiento esperado es menor que r, la estrategia es esencialmente inútil. Ten en cuenta que existen alternativas a los bonos del Tesoro, como LIBOR o la Tasa Preferencial, que pueden ser más adecuadas en ciertos casos.
      • t = tiempo hasta el vencimiento
        El tiempo de vencimiento es simplemente el período restante hasta el vencimiento de la opción, calculado anualmente.
      • x = precio de ejercicio
        El precio de ejercicio de una opción es el precio al que el titular puede ejercer la opción.
      • s = precio del activo subyacente
        s representa el precio del activo subyacente en el momento en que queremos resolver la ecuación.
      • σ = volatilidad
        σ es la última variable en esta ecuación porque generalmente es la que no conocemos y estamos tratando de encontrar. Al ingresar las otras variables en la ecuación, podemos deducir la volatilidad esperada o Volatilidad Implícita (IV) o sigma (σ). Ten en cuenta que la IV se deriva de los precios de las opciones y otras variables, no al revés.

IV vs HV:

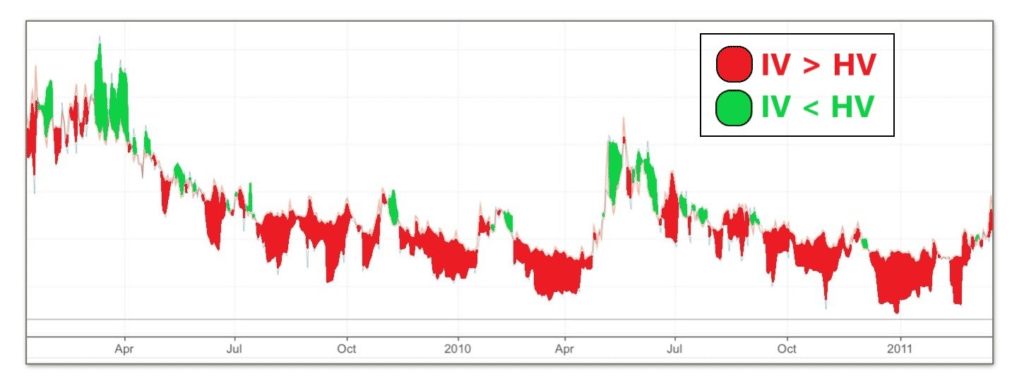
Sin embargo, el tiempo ha demostrado que la ecuación tiene sus límites: el modelo parece sobrestimar consistentemente la volatilidad. Desde 1990, la IV ha sobrestimado el 83% de los días de rendimiento del S&P 500. En otras palabras, la volatilidad esperada (IV) es aproximadamente 4 a 5 veces mayor que la volatilidad histórica (HV).
Estos diversos gráficos también tienen como objetivo ilustrar mi punto: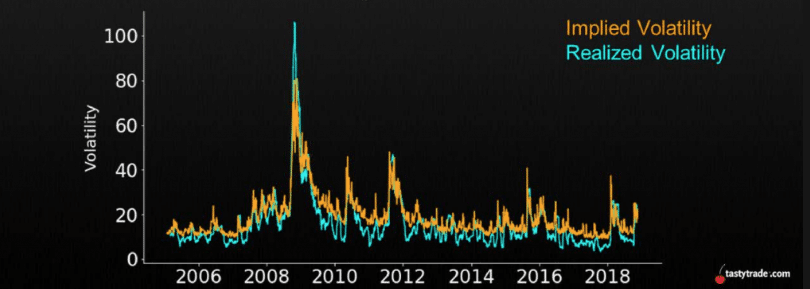

Es posible especular sobre la razón de esta discrepancia. Algunos dicen que se debe a la necesidad constante de las empresas o fondos de cubrirse, lo que empuja la demanda de opciones de venta al alza, llevando al modelo Black-Scholes a exagerar estas situaciones. Otros creen que es prueba de una teoría tan falible como teórica, o que las condiciones óptimas del mercado (eficiencia del mercado) no siempre se cumplen. También se podría considerar la condición de los costos, que no se cumple debido a la falta de liquidez en los mercados para algunos fondos.
La verdad es que la consecuencia directa de interpretar esta estadística lleva a una conclusión más simple: los vendedores de opciones siempre tienen una ligera ventaja estadística sobre los compradores.
Ten cuidado, esta ventaja es puramente estadística y empírica: la historia puede repetirse o cambiar, lo que sucedió ayer puede no necesariamente suceder mañana. Es posible que este año y por algún tiempo, los vendedores de opciones puedan estar en desventaja, ya que lo contrario también puede ser cierto.
En resumen, depende de la interpretación individual determinar si y cuándo se repetirá la historia.