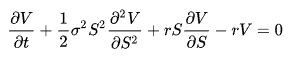Le trading d’Options

Vendre des Options

Une erreur courante chez les traders débutants lorsqu’ils commencent à spéculer sur l’achat ou la vente d’options est de penser que la vente d’options est de « l’argent facile ». La raison pour laquelle beaucoup tombent dans ce piège est simple : selon de nombreuses sources, « 90% des options expirent sans valeur ». Voyons rapidement pourquoi cette statistique est trompeuse avant de vous présenter les subtilités de la vente d’options.

En effet, les données du Chicago Board Options Exchange (CBOE) indiquent que seulement 10% de toutes les options sont réellement exercées (la plupart des traders d’options achètent des options pour spéculer sur leur valeur, pas pour les exercer sur la valeur sous-jacente, d’où le faible nombre), plus de 60% sont clôturées avant l’expiration (encore une fois, la plupart des traders d’options achètent des options pour spéculer dessus, pas pour les conserver jusqu’à l’expiration), et seulement environ 30% expirent sans valeur. Par conséquent, la vente d’options est bien plus complexe qu’il n’y paraît.

Avant toute chose, un rappel sur la nature de la vente d’options est certainement utile pour les débutants :

Alors, qu’est-ce que la vente d’options ?

Rappelez-vous la définition d’une option : c’est un produit qui donne à l’acheteur le droit d’acheter ou de vendre l’actif sous-jacent s’il expire ITM, en échange d’une prime payée pour espérer ce droit.

En d’autres termes, vous payez une prime pour acheter un droit, et inversement, vous êtes payé une prime lorsque vous vendez ce droit. Essentiellement, vous êtes exposé à l’obligation de remplir votre part du contrat si l’option expire ITM.

Vendre une option signifie simplement parier qu’elle expirera OTM, et donc sans valeur. C’est pourquoi ce produit peut être plus intéressant dans certains cas que dans d’autres.

Typiquement, vous comprendrez que la dynamique de l’offre et de la demande sur le marché des options est similaire à celle des marchés « traditionnels » : une partie fait un pari et paie une autre partie pour prendre le pari opposé. Si l’un gagne, l’autre perd, et ainsi de suite.

Avec les options, des facteurs supplémentaires sont le temps et la volatilité, que nous aborderons plus tard.

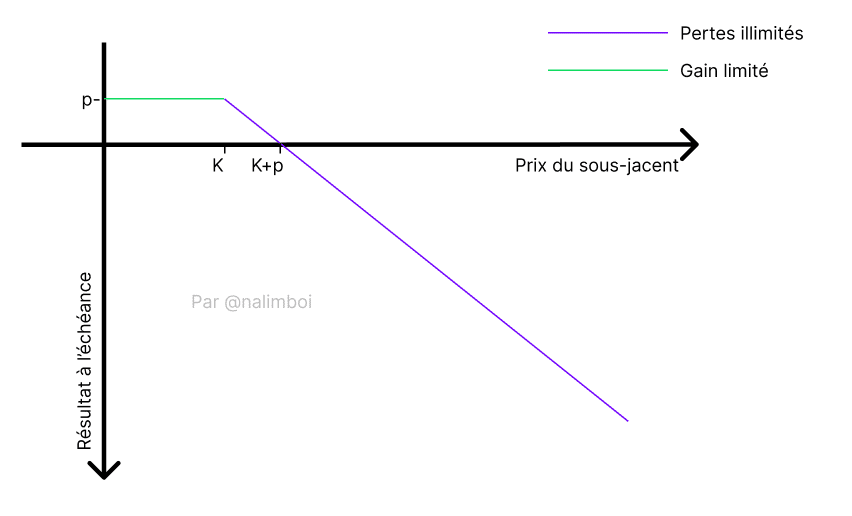
Voici une représentation graphique de ce pari lors de la vente d’une option d’achat : tant que le vendeur d’option ne voit pas le prix d’exercice dépassé (ici K), il conserve ses bénéfices issus de la vente de primes à l’acheteur d’option. K est le prix d’exercice et p est la prime.

Il est facile de voir que dans le cas de la vente d’options, les profits sont confortables lorsque l’option expire OTM mais restent limités. Souvent, vous verrez l’expression « collecter des primes » pour indiquer une vente d’option réussie pour le vendeur.

Cependant, les pertes peuvent être potentiellement illimitées. Le danger est principalement de croire que la vente d’options représente de « l’argent facile ».

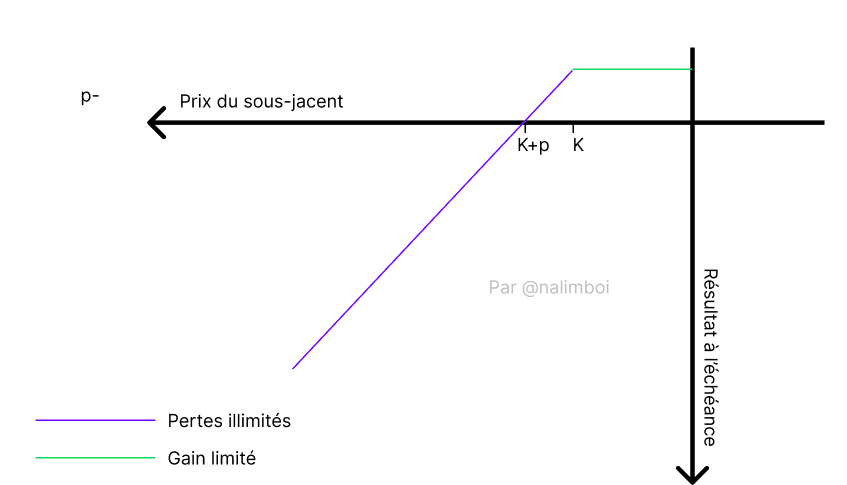
Maintenant, pour voir la différence entre les deux possibilités de vente d’options, voici celle de la vente d’une option de vente :

Comprenez que la vente d’options vous expose grandement à la volatilité, et plus la date d’expiration est éloignée, plus vous risquez de devoir remplir votre part du contrat.

Mais que se passe-t-il si votre prédiction s’avère fausse et que l’option expire ITM ?

Volatilité

En fait, lorsque vous spéculez sur les prix des options, vous spéculez principalement sur la volatilité anticipée ou attendue (IV = Volatilité Implicite).

En d’autres termes, plus la volatilité attendue est élevée, plus les options hors de la monnaie (OTM) deviennent chères, et inversement : plus la volatilité anticipée par le marché est faible, plus les options à la monnaie (ATM) sont chères.

Mais d’abord, revenons aux bases : qu’est-ce que la volatilité ?

Selon Wikipédia, « La volatilité est l’ampleur des variations du cours d’un actif financier. Elle sert de paramètre de quantification du risque de rendement et de prix d’un actif financier. Lorsque la volatilité est élevée, la possibilité de gain est plus importante, mais le risque de perte l’est également. »

La volatilité est un concept qui semble simple à première vue, mais attention à ne pas la confondre avec le volume, qui sont deux choses différentes.

La volatilité attendue (IV) est le résultat de calculs et de la perception globale du marché des mouvements futurs sur les marchés. Elle sert ainsi de moyen de se protéger contre les pertes potentielles lors de la couverture ou de s’exposer lors de la spéculation et de maximiser les gains.

Mais comment est-elle calculée ?

Malgré son apparence complexe, cette équation est probablement l’une des plus grandes avancées de la finance de marché moderne et a permis aux mathématiciens qui l’ont formulée d’introduire la tarification des options dans les stratégies des grands acteurs.

Black-Scholes sert de base à de nombreuses façons de comprendre la volatilité sur les marchés. C’est à partir de cette équation que l’IV peut être calculée. Heureusement pour vous, vous n’aurez probablement pas besoin d’utiliser directement cette équation car de nombreux sites web ou applications s’en chargent déjà.

Plusieurs conditions sont nécessaires pour que la formule soit la plus proche possible de la réalité :

Conditions :

1. 1. 1. Les rendements moyens de l’actif étudié doivent être distribués de manière ‘normale’ ou ‘log-normale’ (voir la section sur la distribution normale).
      2. Le marché étudié est efficient, et donc par définition, les mouvements sont aléatoires (voir la section sur l’efficience des marchés).
      3. Il y a des coûts d’entrée ou de sortie minimes ou nuls ; aucun acteur ne devrait être découragé de prendre position en raison des frais.
      4. L’option est européenne, ce qui signifie qu’elle ne peut être exercée qu’à l’expiration.

Cependant, comme vous pouvez le deviner, ces conditions ne sont pas toujours réunies simultanément. Cela peut entraîner un calcul de l’IV parfois biaisé, ce dont nous discuterons plus en détail ci-dessous.

Maintenant, examinons les variables impliquées dans la résolution de l’équation :

Variables :

1. 1. • r = taux d’intérêt sans risque
        r est le taux d’intérêt auquel on peut investir et générer des revenus sans risque dans l’économie. Dans la plupart des cas, le calcul est effectué à l’aide des bons du Trésor car ils représentent l’un des rares investissements ‘sans risque’. Cette variable est utilisée pour déterminer si une stratégie est viable sur un an : si la stratégie implique un risque et que le rendement attendu est inférieur à r, la stratégie est essentiellement inutile. Notez qu’il existe des alternatives aux bons du Trésor comme le LIBOR ou le Prime Rate, qui peuvent être plus appropriés dans certains cas.
      • t = temps jusqu’à l’expiration
        Le temps d’expiration est simplement la période restante jusqu’à l’expiration de l’option, calculée annuellement.
      • x = prix d’exercice
        Le prix d’exercice d’une option est le prix auquel l’option peut être exercée par son détenteur.
      • s = prix de l’actif sous-jacent
        s représente le prix de l’actif sous-jacent au moment où nous voulons résoudre l’équation.
      • σ = volatilité
        σ est la dernière variable de cette équation car c’est généralement celle que nous ne connaissons pas et que nous essayons de trouver. En entrant les autres variables dans l’équation, nous pouvons déduire la volatilité attendue ou Volatilité Implicite (IV) ou sigma (σ). Sachez que l’IV est dérivée des prix des options et des autres variables, et non l’inverse.

IV vs HV :

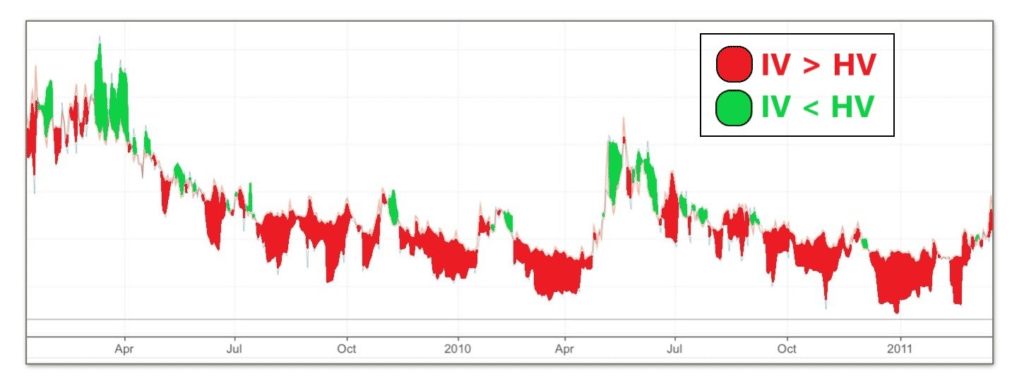
Cependant, le temps a montré que l’équation a ses limites : le modèle semble constamment surestimer la volatilité. Depuis 1990, l’IV a surestimé 83% des jours de rendement du S&P 500. En d’autres termes, la volatilité attendue (IV) est environ 4 à 5 fois plus élevée que la volatilité historique (HV).

Ces différents graphiques visent également à illustrer mon propos :

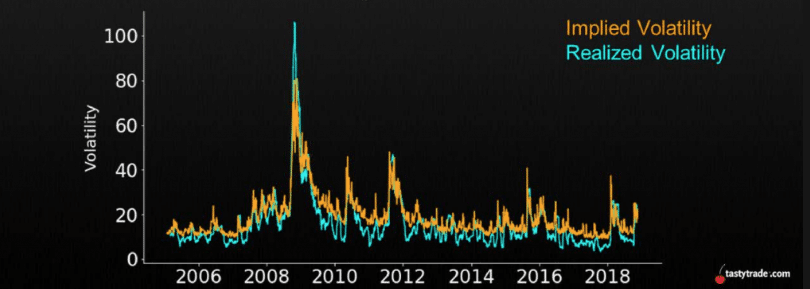
Il est possible de spéculer sur la raison de cet écart. Certains disent que c’est dû au besoin constant des entreprises ou des fonds de se couvrir, ce qui pousse la demande d’options de vente à la hausse, amenant le modèle Black-Scholes à exagérer ces situations. D’autres pensent que c’est la preuve d’une théorie aussi faillible que théorique, ou que les conditions optimales du marché (efficience du marché) ne sont pas toujours réunies. On pourrait aussi considérer la condition des coûts, qui n’est pas remplie en raison du manque de liquidité sur les marchés pour certains fonds.

La vérité est que la conséquence directe de l’interprétation de cette statistique mène à une conclusion plus simple : les vendeurs d’options ont toujours un léger avantage statistique sur les acheteurs.

Soyez prudent, cet avantage est purement statistique et empirique : l’histoire peut se répéter ou changer, ce qui s’est passé hier ne se reproduira pas forcément demain. Il est possible que cette année et pendant un certain temps, les vendeurs d’options soient désavantagés, comme l’inverse peut aussi être vrai.

En bref, c’est à l’interprétation individuelle de déterminer si et quand l’histoire se répétera.