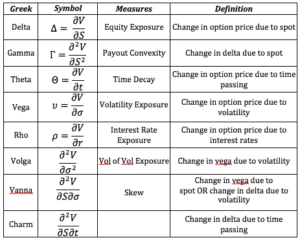
Les Grecs

Les soi-disant Grecs sont des indicateurs de la sensibilité du prix d’une option aux facteurs qui le déterminent, tels que la volatilité ou la valeur de l’actif sous-jacent.

Les Grecs sont utilisés dans l’analyse de sensibilité des options et permettent aux traders de mesurer et d’évaluer l’impact de chaque mouvement de prix de l’actif sous-jacent sur le prix de l’option. De nombreux fonds d’investissement basent leurs stratégies sur ces valeurs.

En termes plus simples, ils nous aident à comprendre comment le prix de l’option réagit lorsque l’actif sous-jacent présente différents « comportements », en changeant une ou plusieurs variables tout en gardant les autres constantes.

Ils servent d’indicateurs pour la prévision et peuvent être très utiles, mais il est essentiel de comprendre qu’il s’agit d’estimations théoriques et donc faillibles.

Comprenez que derrière chaque stratégie directionnelle se cache un jeu de probabilités ; le but n’est pas d’avoir raison à chaque fois mais de gagner de l’argent. L’objectif est toujours de minimiser le risque et de maximiser le profit potentiel.

Delta (Δ)

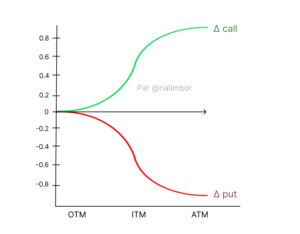
C’est probablement la mesure que vous verrez le plus souvent car elle est très utile et offre de nombreuses applications. Δ mesure le changement du prix d’une option lorsque la valeur de l’actif sous-jacent augmente ou diminue. En d’autres termes, la valeur de l’option changera si le marché monte ou descend d’1 point. Ici, nous voulons savoir de combien cette variation change le prix de l’option concernée. Δ détermine la valeur des options d’achat (positive) et de vente (négative) avec le même prix d’exercice. Le delta pour une option de vente est donc entre 0 et -1, et pour une option d’achat, entre 0 et 1. Il peut aussi être représenté comme : Δ = ∂S/∂V Dans une stratégie d’investissement sous couverture, Δ indique combien de cryptos vous devez acheter (ou vendre) pour vous protéger des mouvements de prix de l’actif sous-jacent. Par exemple, si une option crypto a un delta de 0,45 et que le prix du tokenToken Un actif numérique émis sur une blockchain qui représente divers services publics, droits ou titres. sous-jacent augmente de 1$, la valeur de l’option sur ce token augmentera théoriquement de 0,45$.

Le delta a donc trois utilisations :

• Δ est une mesure de risque estimant la variation du prix de l’option pour un changement de 1$ de son actif sous-jacent.
• Δ indique aux traders le ratio de couverture pour rendre une position delta neutre.
• Δ peut aussi servir d’indicateur en termes de probabilité qu’une option expire ITM. Cependant, statistiquement, plus une option est éloignée de sa date d’expiration et plus elle est volatile, moins Δ est fiable pour mesurer la probabilité que l’option expire ITM.

Thêta (θ)

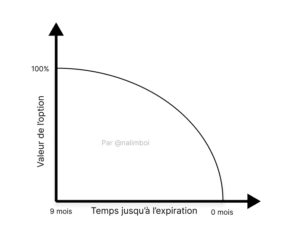
Cette variable exprime de combien le prix ou la prime d’un contrat d’option diminuera avec le temps. En fait, la valeur d’une option tend à diminuer à mesure qu’elle s’approche de son expiration.

Ce paramètre est toujours négatif car il indique la perte de la valeur temporelle d’une option plutôt que sa valeur intrinsèque. Il est relativement facile d’observer que plus la date d’expiration est éloignée, plus la valeur de l’option est élevée.

Essentiellement, c’est une question de probabilités : la chance que l’option expire au-delà du prix d’exercice augmente à mesure que l’incertitude grandit pour le vendeur d’option de l’autre côté de la transaction.

À l’inverse, plus la date d’expiration est proche, plus la probabilité que l’option expire OTM est élevée. Par conséquent, vous pouvez observer la pertinence de θ dans le prix d’une option. La variable est utile pour comprendre que le temps travaille constamment contre l’acheteur d’option et pour évaluer cet effet sur la valeur de l’option.

Pour des temps de plus en plus longs, toute option a une chance tout aussi croissante d’atteindre son prix d’exercice, quelle que soit sa valeur.

Gamma (Γ)

Il quantifie essentiellement de combien la valeur de l’actif sous-jacent ou de l’action change lorsque Delta change. D’un côté, Δ rend compte du changement de la prime de l’option, tandis que Γ indique le taux de changement de Δ.

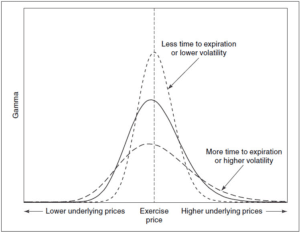
Mathématiquement, Gamma est intuitivement la première dérivée de Delta. La lettre grecque est graphiquement similaire à une forme log-normale de la fonction Delta. Ainsi, il est intéressant de noter que plus l’expiration est éloignée, plus la courbe Gamma tend à s’aplatir.

À l’inverse, à mesure que l’expiration approche, Gamma tend à gagner ou perdre rapidement de la valeur avec des changements de prix de plus en plus mineurs, rendant sa structure plus raide et formant parfois même un ‘pic’ lorsque l’expiration est très proche. La volatilité joue également un rôle similaire, maintenant la relation : plus la volatilité est élevée, plus la courbe est plate, et vice versa.

Rho (ρ)

Il calcule le changement du prix de l’option causé par une augmentation ou une diminution des taux d’intérêt sans risque, exprimé en pourcentage. Les options de vente ont souvent un rho négatif, tandis que les options d’achat ont fréquemment un rho positif.

C’est la mesure qui quantifie le changement du prix de l’option lorsque r, le taux d’intérêt, varie également.

C’est probablement l’une des mesures qui varient le moins dans le temps ; cependant, elle joue un rôle majeur pendant les crises ou les périodes de resserrement car il devient de plus en plus difficile de maintenir un r bas. Cela impacte nécessairement la façon dont l’IV est calculée puisqu’elle est la sortie générée par l’équation. Ainsi, changer ne serait-ce qu’une variable modifie inévitablement le résultat.

Vega (v)

Il mesure comment une augmentation ou une diminution de la Volatilité Implicite (IV) de l’actif sous-jacent ou de l’action modifierait le prix de l’option (prime).

En d’autres termes, une plus grande volatilité attendue augmente la valeur des puts et des calls, tandis qu’une volatilité attendue plus faible diminue leur valeur (voir la section sur la volatilité).

Vega tend à prévoir ce changement, étant une dérivée du changement attendu de l’IV.

Vega prend une forme de distribution normale et tend à s’aplatir à mesure que l’expiration approche.