Greeks

The so-called Greeks are indicators of an option’s price sensitivity to factors that determine it, such as volatilityVolatility The degree of variation in an asset's price over time. or the value of the underlying assetAsset Any digital asset, including cryptocurrencies..

The Greeks are used in option sensitivity analysis and allow traders to measure and assess the impact of each price movement of the underlying asset on the option’s price. Many investment funds base their strategies on these values.

In simpler terms, they help us understand how the option price reacts when the underlying asset exhibits different “behaviors,” when changing one or more variables while keeping others constant.

They serve as indicators for forecasting and can be very useful, but it is essential to understand that they are theoretical estimates and thus fallible.

Understand that behind every directional strategy lies a game of probability; the goal is not to be right every time but to make money. The aim is always to minimize risk and maximize potential profit.

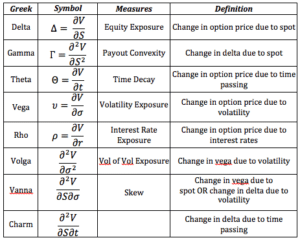
Delta (Δ)

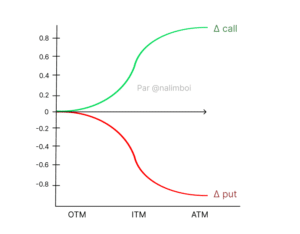
This is probably the measure you will see most often because it is very useful and offers many applications. Δ measures the change in the price of an option when the value of the underlying asset increases or decreases. In other words, the option’s value will change if the marketMarket A place where assets are bought and sold. moves up or down by 1 point. Here, we want to know how much this variation changes the price of the concerned option. Δ determines the value of call (positive) and put (negative) options with the same strike price. The delta for a put is thus between 0 and -1, and for a call, between 0 and 1. It can also be represented as: Δ = ∂S/∂V In an investment strategy under hedge, Δ indicates how many cryptos you need to buy (or sell) to protect yourself from price movements of the underlying asset. For example, if a crypto option has a delta of 0.45 and the underlying tokenToken A digital asset issued on a blockchain, representing various utilities, rights, or value.’s price increases by $1, the value of the option on that token will theoretically increase by $0.45.

The delta thus has three uses:

• Δ is a risk measure estimating the option price variation for a $1 change in its underlying asset.
• Δ tells traders the hedge ratio to make a position delta neutral.
• Δ can also serve as an indicator in terms of the probability of an option expiring ITM. However, statistically, the further an option is from its expiration date and the more volatile it is, the less reliable Δ is at measuring the probability that the option will expire ITM.

Thêta (θ)

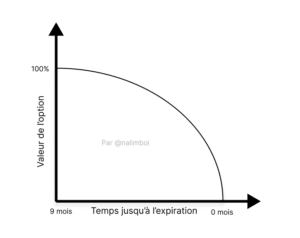
This variable expresses how much the price or premium of an option contract will decrease over time. In fact, the value of an option tends to decrease as it approaches its expiration.

This parameter is always negative because it indicates the loss of the time value of an option rather than its intrinsic value. It is relatively easy to observe that the further the expiration date, the higher the value of the option.

Essentially, it’s a matter of probabilities: the chance that the option will expire beyond the strike price increases as uncertainty grows for the option seller on the other side of the trade.

Conversely, the closer the expiration date, the higher the probability that the option will expire OTM. Therefore, you can observe θ’s relevance in the price of an option. The variable is useful to understand that time constantly works against the option buyer and to assess this effect on the option’s value.

For increasingly longer times, any option has an equally increasing chance of reaching its strike price, regardless of its value.

Gamma (Γ)

It essentially quantifies how much the value of the underlying asset or stock changes when Delta changes. On one hand, Δ accounts for the change in the option’s premium, while Γ indicates the rate of change of Δ.

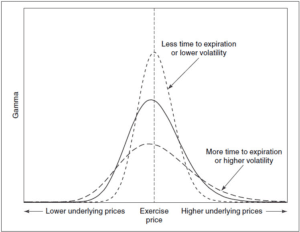
Mathematically, Gamma is intuitively the first derivative of Delta. The Greek letter is graphically similar to a log-normal form of the Delta function. Thus, it is interesting to note that the further away the expiration is, the more the Gamma curve tends to flatten.

Conversely, as expiration approaches, Gamma tends to rapidly gain or lose value with increasingly minor price changes, making its structure steeper and sometimes even forming a ‘peak’ when expiration is very near. Volatility also plays a similar role, maintaining the relationship: the higher the volatility, the flatter the curve, and vice versa.

Rho (ρ)

It calculates the change in the option price caused by an increase or decrease in risk-free interest rates, expressed as a percentage. Put options often have a negative rho, while call options frequently have a positive rho.

It is the measure that quantifies the change in the option price when r, the interest rate, also varies.

It is probably one of the measures that vary the least over time; however, it plays a major role during crises or tightening periods as it becomes increasingly difficult to maintain a low r. This necessarily impacts the way IV is calculated since it is the output generated by the equation. Thus, changing even one variable inevitably alters the result.

Vega (v)

It measures how an increase or decrease in the Implied Volatility (IV) of the underlying asset or stock would modify the option price (premium).

In other words, greater expected volatility increases the value of both puts and calls, while lower expected volatility decreases their value (see the section on volatility).

Vega tends to forecast this change, being a derivative of the expected change in IV.

Vega takes on a normal distribution shape and tends to flatten as expiration approaches.