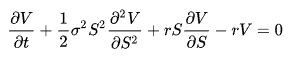A negociação de Opções

Venda de Opções

Um erro comum entre traders iniciantes quando começam a especular na compra ou venda de opções é pensar que vender opções é “dinheiro fácil”. A razão pela qual muitos caem nessa armadilha é simples: de acordo com muitas fontes, “90% das opções expiram sem valor”. Vamos ver rapidamente por que essa estatística é enganosa antes de apresentar as complexidades da venda de opções.
De fato, dados da Chicago Board Options Exchange (CBOE) indicam que apenas 10% de todas as opções são realmente exercidas (a maioria dos traders de opções compra opções para especular sobre seu valor, não para exercê-las sobre o valor subjacente, daí o baixo número), mais de 60% são fechadas antes do vencimento (novamente, a maioria dos traders de opções compra opções para especular sobre elas, não para mantê-las até o vencimento), e apenas cerca de 30% expiram sem valor. Portanto, vender opções é muito mais complexo do que parece.
Antes de mais nada, uma revisão sobre a natureza da venda de opções é certamente útil para iniciantes:

Então, o que é vender opções?

Lembre-se da definição de uma opção: é um produto que dá ao comprador o direito de comprar ou vender o ativo subjacente se expirar ITM, em troca de um prêmio pago para esperar por esse direito.
Em outras palavras, você paga um prêmio para comprar um direito e, inversamente, você é pago um prêmio quando vende esse direito. Essencialmente, você está exposto à obrigação de cumprir sua parte do contrato se a opção expirar ITM.
Vender uma opção simplesmente significa apostar que ela expirará OTM, e assim sem valor. É por isso que este produto pode ser mais interessante em alguns casos do que em outros.
Tipicamente, você entenderá que a dinâmica de oferta e demanda no mercado de opções é semelhante à dos mercados “tradicionais”: uma parte faz uma aposta e paga outra parte para fazer a aposta oposta. Se um ganha, o outro perde, e assim por diante.
Com opções, fatores adicionais são o tempo e a volatilidade, que abordaremos mais tarde.
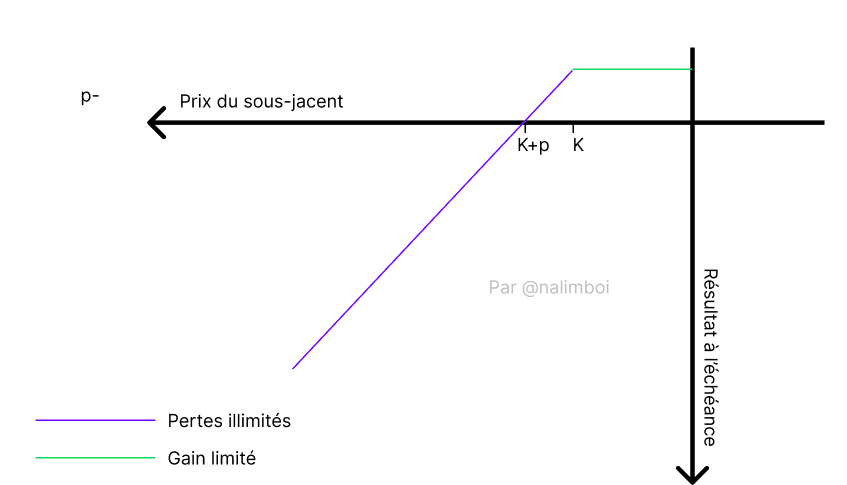
Aqui está uma representação gráfica dessa aposta ao vender uma opção de compra: enquanto o vendedor da opção não vir o preço de exercício ultrapassado (aqui K), ele mantém seus lucros da venda de prêmios para o comprador da opção. K é o preço de exercício e p é o prêmio.

É fácil ver que no caso de vender opções, os lucros são confortáveis quando a opção expira OTM, mas permanecem limitados. Frequentemente, você verá a expressão “coletar prêmios” para indicar uma venda de opção bem-sucedida para o vendedor.

No entanto, as perdas podem ser potencialmente ilimitadas. O perigo é principalmente acreditar que vender opções representa “dinheiro fácil”.

Agora, para ver a diferença entre as duas possibilidades de vender opções, aqui está a de vender uma opção de venda:

Entenda que vender opções o expõe grandemente à volatilidade, e quanto mais distante a data de vencimento, mais provável é que você tenha que cumprir sua parte do contrato.
Mas o que acontece se sua previsão se mostrar errada e a opção expirar ITM?

Volatilidade

Na verdade, quando você especula sobre os preços das opções, você está principalmente especulando sobre a volatilidade antecipada ou esperada (IV = Volatilidade Implícita).
Em outras palavras, quanto maior a volatilidade esperada, mais caras se tornam as opções fora do dinheiro (OTM), e o mesmo acontece ao contrário: quanto menor a volatilidade antecipada pelo mercado, mais caras são as opções no dinheiro (ATM).
Mas primeiro, vamos voltar ao básico: o que é volatilidade?
Segundo a Wikipedia, “Volatilidade é a extensão das variações no preço de um ativo financeiro. Serve como um parâmetro para quantificar o risco de retorno e preço de um ativo financeiro. Quando a volatilidade é alta, a possibilidade de ganho é maior, mas o risco de perda também é maior.”
Volatilidade é um conceito que parece simples à primeira vista, mas cuidado para não confundi-la com volume, que são duas coisas diferentes.
A volatilidade esperada (IV) é o resultado de cálculos e da percepção geral do mercado sobre movimentos futuros nos mercados. Assim, serve como um meio de se proteger contra possíveis perdas ao fazer hedge ou se expor ao especular e maximizar ganhos.
Mas como é calculada?

Apesar de sua aparência complexa, esta equação é provavelmente um dos maiores avanços nas finanças de mercado modernas e permitiu que os matemáticos que a formularam introduzissem a precificação de opções nas estratégias dos grandes players.
Black-Scholes serve como base para muitas maneiras de entender a volatilidade nos mercados. É a partir desta equação que a IV pode ser calculada. Felizmente para você, provavelmente não precisará usar esta equação diretamente, pois muitos sites ou aplicativos já lidam com isso.
Várias condições são necessárias para que a fórmula seja o mais próxima possível da realidade:
Condições:

1. 1. 1. Os retornos médios do ativo estudado devem ser distribuídos de maneira ‘normal’ ou ‘log-normal’ (veja a seção sobre distribuição normal).
      2. O mercado estudado é eficiente e, portanto, por definição, os movimentos são aleatórios (veja a seção sobre eficiência de mercado).
      3. Há custos de entrada ou saída mínimos ou nulos; nenhum ator deve ser desencorajado a tomar uma posição devido a taxas.
      4. A opção é europeia, o que significa que só pode ser exercida no vencimento.

No entanto, como você pode adivinhar, essas condições nem sempre são atendidas simultaneamente. Isso pode resultar em um cálculo de IV às vezes tendencioso, o que discutiremos mais adiante.
Agora, vamos olhar para as variáveis envolvidas na resolução da equação:

Variáveis:

1. 1. • r = taxa de juros livre de risco
        r é a taxa de juros na qual se pode investir e gerar renda livre de risco na economia. Na maioria dos casos, o cálculo é feito usando títulos do Tesouro, pois representam um dos poucos investimentos ‘livres de risco’. Esta variável é usada para determinar se uma estratégia é viável ao longo de um ano: se a estratégia envolve risco e o retorno esperado é menor que r, a estratégia é essencialmente inútil. Note que existem alternativas aos títulos do Tesouro, como LIBOR ou a Taxa Preferencial, que podem ser mais adequadas em certos casos.
      • t = tempo até o vencimento
        O tempo de vencimento é simplesmente o período restante até o vencimento da opção, calculado anualmente.
      • x = preço de exercício
        O preço de exercício para uma opção é o preço no qual a opção pode ser exercida pelo seu titular.
      • s = preço do ativo subjacente
        s representa o preço do ativo subjacente no momento em que queremos resolver a equação.
      • σ = volatilidade
        σ é a última variável nesta equação porque geralmente é aquela que não conhecemos e estamos tentando encontrar. Ao inserir as outras variáveis na equação, podemos deduzir a volatilidade esperada ou Volatilidade Implícita (IV) ou sigma (σ). Esteja ciente de que a IV é derivada dos preços das opções e outras variáveis, não o contrário.

IV vs HV:

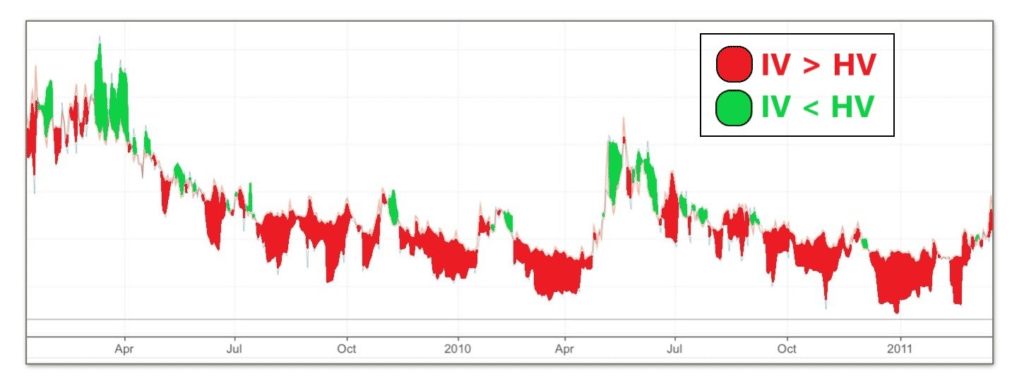
No entanto, o tempo mostrou que a equação tem seus limites: o modelo parece consistentemente superestimar a volatilidade. Desde 1990, a IV superestimou 83% dos dias de retorno do S&P 500. Em outras palavras, a volatilidade esperada (IV) é cerca de 4 a 5 vezes maior que a volatilidade histórica (HV).
Estes vários gráficos também visam ilustrar meu ponto:

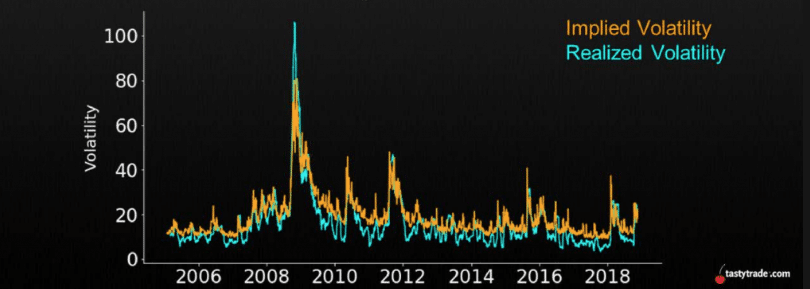
É possível especular sobre a razão desta discrepância. Alguns dizem que é devido à necessidade constante de empresas ou fundos de fazer hedge, o que empurra a demanda por opções de venda para cima, levando o modelo Black-Scholes a exagerar essas situações. Outros acreditam que é prova de uma teoria tão falível quanto teórica, ou que as condições ótimas de mercado (eficiência de mercado) nem sempre são atendidas. Pode-se também considerar a condição de custos, que não é atendida devido à falta de liquidez nos mercados para alguns fundos.
A verdade é que a consequência direta de interpretar esta estatística leva a uma conclusão mais simples: os vendedores de opções sempre têm uma ligeira vantagem estatística sobre os compradores.
Seja cauteloso, esta vantagem é puramente estatística e empírica: a história pode se repetir ou mudar, o que aconteceu ontem pode não necessariamente acontecer amanhã. É possível que este ano e por algum tempo, os vendedores de opções possam estar em desvantagem, assim como o oposto também pode ser verdadeiro.
Em resumo, cabe à interpretação individual determinar se e quando a história se repetirá.